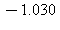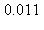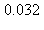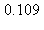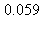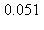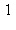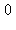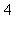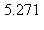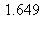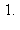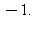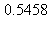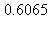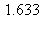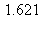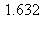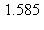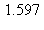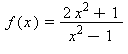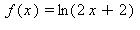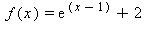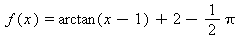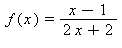AP Calculus Practice Exam
AB Version - Section I - Part B
Calculators ARE Permitted On This Portion Of The Exam
17 Questions - 50 Minutes
1) Give a value of c that satisfies the conclusion of the Mean Value Theorem for Derivatives for the function on the interval [1,3].
on the interval [1,3].
a) 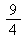
b) 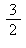
c) 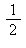
d) 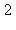
e) 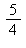
2) The function is invertible. Give the derivative of f -1 at x = 2.
is invertible. Give the derivative of f -1 at x = 2.
a) 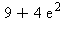
b) 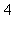
c) 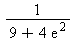
d) 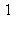
e) 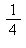
3) The derivative of f is graphed below. Give a value of x where f has a local maximum.
Give a value of x where f has a local maximum.
a) 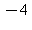
b) 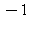
c) 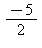
d) 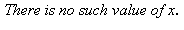
e) 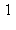
4) Let  Which of the following is (are) true?
Which of the following is (are) true?1) f is continuous at x = -2.
2) f is differentiable at x = 1.
3) f has a local minimum at x = 0.
4) f has an absolute maximum at x = -2.
a) 2 and 4
b) 3 only
c) 2 only
d) 1 and 3
e) 1 and 4
5) Given Determine
Determine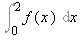
a) 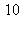
b) 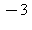
c) 
d) 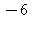
e) 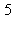
6) Give the approximate location of a local maximum for the function 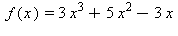
a) 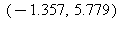
b) 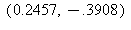
c) 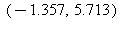
d) 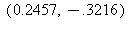
e) 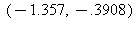
7) Give the approximate average value of the function over the interval [1,4].
over the interval [1,4].
a) 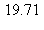
b) 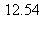
c) 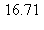
d) 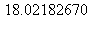
e) 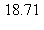
8) The region enclosed by the graphs of  is rotated around the y-axis to generate a solid. What is the volume of the solid?
is rotated around the y-axis to generate a solid. What is the volume of the solid?
a) 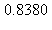
b) 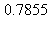
c) 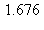
d) 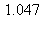
e) 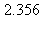
9) What is the approximate instantaneous rate of change of the function at t =
at t = 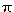 /7?
/7?
a) 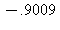
b) 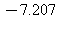
c) 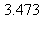
d) 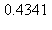
e) 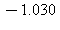
10) What is the error when the integral  is approximated by the Trapezoidal rule with n = 3?
is approximated by the Trapezoidal rule with n = 3?
a) 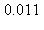
b) 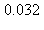
c) 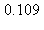
d) 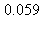
e) 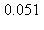
11) The amount of money in a bank account is increasing at the rate of  dollars per year, where t is measured in years. If t = 0 corresponds to the year 2005, then what is the approximate total amount of increase from 2005 to 2007.
dollars per year, where t is measured in years. If t = 0 corresponds to the year 2005, then what is the approximate total amount of increase from 2005 to 2007.
a) $18,350
b) $4,500
c) $21,250
d) $32,560
e) $16,250
12) A particle moves with acceleration and its initial velocity is 0. For how many values of t does the particle change direction?
and its initial velocity is 0. For how many values of t does the particle change direction?
a) 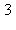
b) 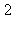
c) 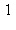
d) 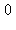
e) 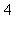
13) At what approximate rate (in cubic meters per minute) is the volume of a sphere changing at the instant when the surface area is 5 square meters and the radius is increasing at the rate of 1/3 meters per minute?
a) 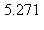
b) 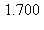
c) 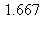
d) 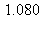
e) 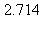
14) A rectangle has one side on the x-axis and the upper two vertices on the graph of  Give a decimal approximation to the maximum possible area for this rectangle.
Give a decimal approximation to the maximum possible area for this rectangle.
a) 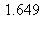
b) 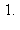
c) 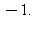
d) 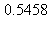
e) 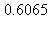
15) A rough approximation for ln(5) is 1.609. Use this approximation and differentials to approximate ln(128/25).
a) 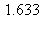
b) 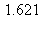
c) 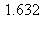
d) 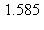
e) 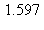
16) The function is differentiable everywhere. What is n?
is differentiable everywhere. What is n?
a) 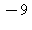
b) 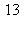
c) 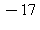
d) 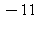
e) 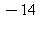
17) Which of the following functions has a vertical asymptote at x = -1 and a horizontal asymptote at y = 2?
a) 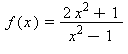
b) 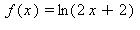
c) 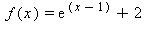
d) 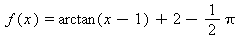
e) 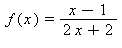


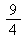
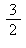
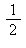
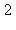
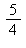

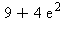
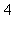
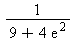
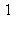
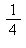

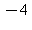
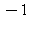
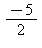
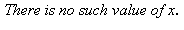
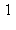


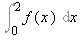
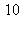
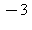
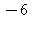
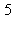
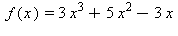
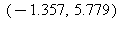
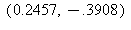
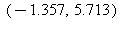
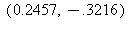
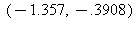

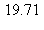
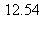
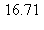
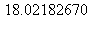
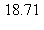

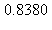
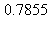
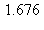
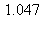
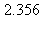

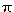 /7?
/7?