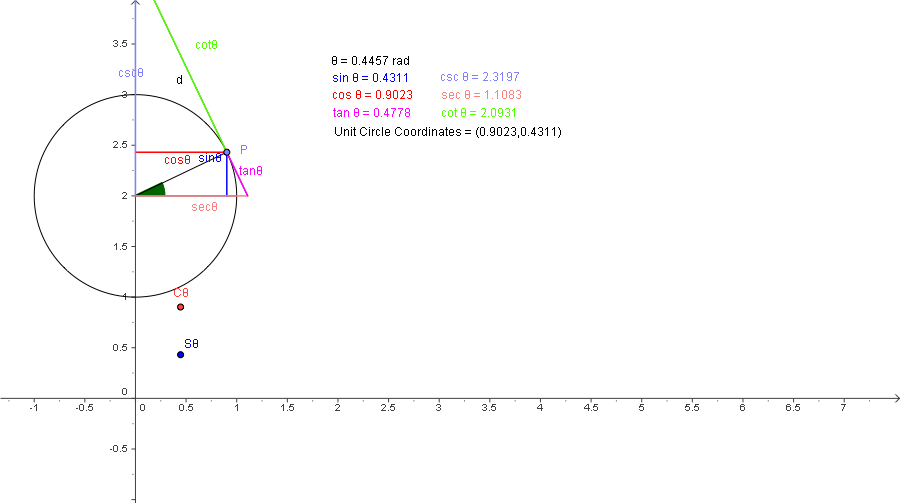

This chart gives the step by step construction used above.
| No. | Name | Definition |
|---|---|---|
| 1 | Point P0 | Point at (0,2), circle shifted up for clarity |
| 2 | Circle UnitCircle | Circle with center P0 and Radius 1 |
| 3 | Point P | Draggable Point on UnitCircle |
| 4 | Text Circle | "Unit Circle Coordinates = (" + (x(P)) + "," + (y(P) - 2) + ")" |
| 5 | Point P1 | Point at (0,2) + (1,0) |
| 6 | Angle θ | Angle between P1, P0, P |
| 7 | Text θ | "θ = " + θ |
| - | - | - |
| 8 | Line L1 | Line through P perpendicular to yAxis |
| 9 | Point P3 | intersection point of L1, yAxis - P moved to y axis |
| 10 | Segment sinθ | Segment[P3, P] |
| 11 | Text sin θ | "sin θ = " + (y(P) - 2) -- Remeber the shift |
| 12 | Point Sθ | (θ, y(P) - 2) -- Traceable sin point |
| - | - | - |
| 13 | Line L2 | Line through P perpendicular to xAxis |
| 14 | Line L3 | Line through P0, P1 - x axis shifted up through P0 |
| 15 | Point P4 | intersection point of L2, L3 |
| 16 | Segment cosθ | Segment[P, P4] |
| 17 | Text cosθ | "cos θ = " + (x(P)) |
| 18 | Point Cθ | (θ, x(P)) -- Traceable cos point |
| - | - | - |
| 19 | Line L4 | Tangent through P to UnitCircle |
| 20 | Point P5 | intersection point of L4, L3 -- tangent-secant point |
| 21 | Segment secθ | Segment[P0, P5] |
| 22 | Text sec θ | "sec θ = " + (x(P5)) |
| 23 | Segment tanθ | Segment[P, P5] |
| 24 | Text tan θ | "tan θ = " + ((y(P) - 2) / x(P)) |
| - | - | - |
| 25 | Point P6 | intersection point of L4, yAxis -- cotangent-cosecant point |
| 26 | Segment cscθ | Segment[P6, P0] |
| 27 | Text csc θ | "csc θ = " + (y(P6) - 2) |
| 28 | Segment cotθ | Segment[P, P6] |
| 29 | Text cot θ | "cot θ = " + (x(P) / (y(P) - 2)) |
Return to the Applets for courses below calculus page.
Return to the Calculus Applet page.
Return to the GeoGebra Applet page.